Rotationsintegrale.: Unterschied zwischen den Versionen
Aus KAS-Wiki
(Die Seite wurde neu angelegt: Ein '''Rotationskörper''' ensteht, indem man eine Fläche um eine Drehachse rotieren lässt. Diese Fläche ist durch eine auf dem Intervall [a; b] stetige Funktion f u...) |
|||
| Zeile 1: | Zeile 1: | ||
| − | Ein '''Rotationskörper''' ensteht, indem man eine Fläche um eine Drehachse rotieren lässt. Diese Fläche ist durch eine auf dem Intervall [a; b] stetige Funktion f und der jeweiligen Achse. | + | Ein '''Rotationskörper''' ensteht, indem man eine Fläche um eine Drehachse rotieren lässt. Diese Fläche ist durch eine auf dem Intervall [a; b] stetige Funktion f, den Gleichungen x=a und x=b und der jeweiligen Achse eingeschlossen. |
| + | |||
| + | [[Bild:Sv74b74c.gif]] | ||
| + | |||
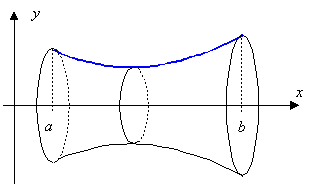
| + | In der obenstehenden Abbildung handelt es sich, um eine Rotation um die x-Achse. Unser Ziel ist es das Volumen der Rotationskörper bei Rotierung um die x- bzw. y-Achse zu berechnen. | ||
Version vom 8. Dezember 2009, 14:26 Uhr
Ein Rotationskörper ensteht, indem man eine Fläche um eine Drehachse rotieren lässt. Diese Fläche ist durch eine auf dem Intervall [a; b] stetige Funktion f, den Gleichungen x=a und x=b und der jeweiligen Achse eingeschlossen.
In der obenstehenden Abbildung handelt es sich, um eine Rotation um die x-Achse. Unser Ziel ist es das Volumen der Rotationskörper bei Rotierung um die x- bzw. y-Achse zu berechnen.