Exponentialfunktionen.: Unterschied zwischen den Versionen
Aus KAS-Wiki
Enes12 (Diskussion | Beiträge) |
Enes12 (Diskussion | Beiträge) |
||
| Zeile 8: | Zeile 8: | ||
D.h.: a > 1 hat die Eigenschaft STRENG MONOTON STEIGERND und 0 < a < 1 hat die Eigenschaft STRENG MONOTON FALLEND. | D.h.: a > 1 hat die Eigenschaft STRENG MONOTON STEIGERND und 0 < a < 1 hat die Eigenschaft STRENG MONOTON FALLEND. | ||
| + | |||
| + | <u>> Die natürliche Exponentialfunktion und ihre Ableitung:</u> | ||
Version vom 12. Dezember 2009, 13:15 Uhr
> Eigenschaften der Funktion:
Die Funktionsgleichung der Exponentialfunktion besteht aus folgender Form:
f(x) = ax oder auch g(x) = cax wobei: c
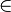
, a > 0, x
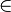
ist.
Die Exponentialfunktion beschreibt für a > 1 einen Wachstumsprozess und für 0 < a < 1 einen Zerfallsprozess.
D.h.: a > 1 hat die Eigenschaft STRENG MONOTON STEIGERND und 0 < a < 1 hat die Eigenschaft STRENG MONOTON FALLEND.
> Die natürliche Exponentialfunktion und ihre Ableitung:
> Ableitung und Integrieren zusammengesetzter Funktionen:
> Untersuchung von Exponentialfunktionen:

