Prozeß- und Übergangsmatizen

Eine Übergangsmatrix beschreibt einen Übergang von einer Dimension in eine andere.

$M*\vec a=\vec a_1$

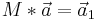
Grenzwert:

$M*\vec a=\vec a$

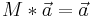
Ein Grenzwert ist dann erreicht, wenn sich die Matrix durch einen Vektor nicht mehr ändert z.B. bei Populationsentwicklungen.

Einheitsmatrix

$E*\vec a=\vec a$

$M^n=M$

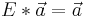
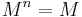
Nach n Jahren tritt wieder der gleiche Zustand ein, ist also zyklisch, wie bei Tierpopulationen.

A+B=(\bigl( \begin{smallmatrix} a_1&a_2 \\ b_1&b_2 \end{smallmatrix} \bigr)