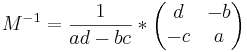Prozeß- und Übergangsmatizen
Aus KAS-Wiki
Version vom 3. Dezember 2009, 10:31 Uhr von Helen H. (Diskussion | Beiträge)
Inhaltsverzeichnis |
Übergangsmatrizen:
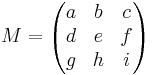
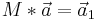
Eine Übergangsmatrix beschreibt einen Übergang von einer Dimension in eine andere.
Addition von Matrizen:
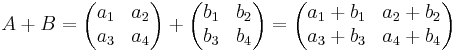
Multiplikation:
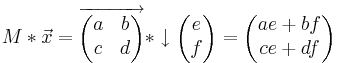
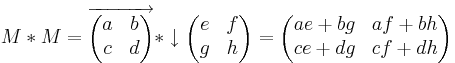
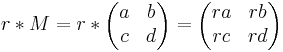
Inverse:
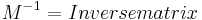
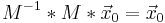
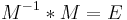
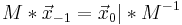
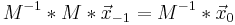
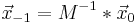
Grenzwert:
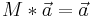
Ein Grenzwert ist dann erreicht, wenn sich die Matrix durch einen Vektor nicht mehr ändert z.B. bei Populationsentwicklungen. Wenn ein Grenzwert existiert, sind alle Spalten gleich, eine Gleichgewichtsverteilung besteht.
Einheitsmatrix:
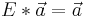
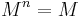
Nach n Jahren tritt wieder der gleiche Zustand ein, ist also zyklisch, wie bei Tierpopulationen.
Übergangsgraph:
Determinanten:
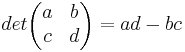
Eine Determinante beschreibt den Übergang von einer Matrix (M) zu einer inversen Matrix (M^-1).
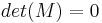 ->dann existiert keine inverse Matrix!
->dann existiert keine inverse Matrix!
Wenn die 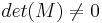 , dann heißt die Matrix affine Abbildung!
, dann heißt die Matrix affine Abbildung!