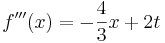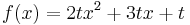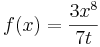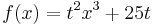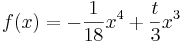Ableitung von Funktionsscharen
Aus KAS-Wiki
Version vom 17. Februar 2011, 21:28 Uhr von Karl Kirst (Diskussion | Beiträge)
Besonderheiten beim Ableiten von Funktionsscharen
Zum besseren Verständnis eignet sich auch das Video:
- Der Parameter t wird wie eine Zahl behandelt
-Beispiel 1:
Die Ableitung einer Zahl ist null, also ist die Ableitung von t ebenfalls null!
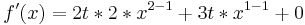
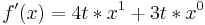
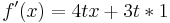
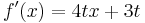
-Beispiel 2:
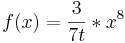
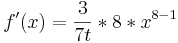
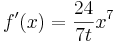
-Beispiel 3:
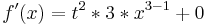
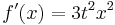
Beispiel zum Video
- Erste Ableitung
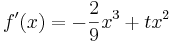
- Zweite Ableitung
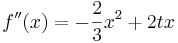
- Dritte Ableitung