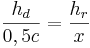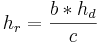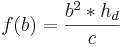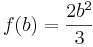Extremwertaufgaben.

Inhaltsverzeichnis

1 Definition:
2 Lösungsansatz:
3 Hilfsmittel:
- 3.1 Formeln aus der Geometrie
4 Beispiele
5 Beispiel 5

Definition:

Extremwertprobleme sind Aufgaben, in denen eine Größe optimiert werden soll. Dazu wird eine Zielgröße mithilfe einer Zielfunktion dargestellt, die meistens von zwei Variablen abhängig ist. Durch Ausnutzen einer Nebenbedingung kann eine der Variablen durch die andere ausgedrückt werden. (Kurvendiskussion)

Lösungsansatz:

Zielfunktion aufstellen.
Prüfen, ob Zielfunktion von Nebenbedingungen abhängt.
Nebenbedingung suchen (Um Variablen in Beziehung zu bringen).
Ableiten. (Ableitungsregeln.)
Extrempunkte bestimmen (Extrempunkte).
Rand des Definitionsbereiches auf globale Extremstellen prüfen. (Grenzverhalten)

Hilfsmittel:

Als Problem der Extremwertaufgaben stellen sich häufig die Nebenbedingungen dar, die nicht immer sofort erkennbar aber unabdingbar sind, um die Aufgaben zu lösen. Da die Zielfunktionen zumeist 2 verschiedene Variablen enthalten, ist es notwendig, eine der beiden Variablen in Abhängigkeit der anderen darzustellen. Wenn man also eine Zielfunktion 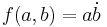$f(a,b)=a \dot b$ hat, wäre das Ergebnis einer Nebenbedingung etwa 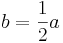$b= \frac{1}{2}a$ woraus sich nun die Zielfunktion in Abhängigkeit von nur einer variable a darstellt, in diesem Fall als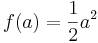 $f(a)= \frac{1}{2}a^2$

Hier finden Sie einen kurzen Abriss gängiger Hilfsmittel zur Findung von Nebenbedingungen:

Formeln aus der Geometrie

1. Volumenformeln: Die Formeln Konstanter Volumen oder Flächengrößen in einer Extremwertaufgabe helfen häufig eine Nebenbedingung zu finden. Wenn man z.B. ein Zylinder mit möglichst großem Volumen innerhalb einer Kugel mit konstantem Volumen darstellen soll kann man die Zielfunktion
2. Satz des Pythagoras:
Wenn man zum Beispiel einen kreis mit konstantem Radius r gegeben hat und darin ein möglichst großes Rechteck bilden soll, so liegt die Nebenbedingung darin, das die Diagonale des Rechtecks gleich des Kreisdurchmessers ist. d=2r Mit dem Satz des Pythagoras lässt sich nun eine Nebenbedingnungsformel formulieren, die eine seite des Rechtecks in abhängigkeit der anderen mit dem faktor r darstellt. 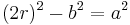$(2r)^2-b^2=a^2$ Das Ergebnis der nach a aufgelösten Formel lässt sich nun in die zielfunktion f(a,b)=a*b einfügen. Diese Aufgabe wird genauer erläutert in Beispiel 3.
3. Sinus-/ Cosinus-/ Tangenssätze:

4. Strahlensatz:

5. Einführung in ein Koordinatensystem:
Siehe Beispiel 2

Beispiele

Beispiel 1

Ein Schäfer benötigt für seine Schafherde ein rechteckigen Pferch mit einem Flächeninhalt von 500m². Wie soll er die Maße des Rechtecks wählen, damit für eine Umzäunung möglichst wenig Material benötigt wird, wenn eine Rechteckseite von einem Bach gebildet wird?

Lösung:

Zielfunktion: U(x)= 2x + 2y, daraus folgt U(x)= x + 2y, da auf einer Seite kein Zaun benötigt wird, weil dort ein Bach verläuft.
Prüfen, ob Zielfunktion von Nebenbedingungen abhängt: Die gesuchte Zielfunktion soll die Seitenlängen des Zauns angeben, bei denen ein möglichst geringer Materialverbrauch, also ein möglichst kleiner Umfang, entsteht. Des Weiteren soll eine Fläche von 500 m² entstehen. Der Umfang ist abhängig vom Flächeninhalt, die Zielfunktion ist also auch abhängig von einer Nebenbedingung.
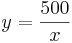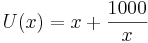Nebenbedingungen suchen: 500= x * y Löst man die bereits aufgestellte Nebenbedingung 500 = x * y nach y auf erhält man $y = \frac {500} {x}$ . Nach einsetzen in U = x + 2y ergibt sich unsere Zielfunktion: $U(x) = x + \frac {1000} {x}$ .
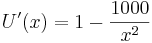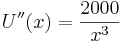Die Ableitungen der Funktion sind: $U'(x)=1-\frac {1000} {x^2}$ und $U''(x)= \frac {2000} {x^3}$ .
Extrempunkte bestimmen: Für U' (x) = 0 erhält man x = 31,622, das sich aufgrund der Bedingung U (31,622) > 0 als Tiefpunkt herausstellt.
Rand des Definitionsbereiches prüfen: Für x=0 würde die Seite wegfallen und für x=500 hätte man einen zu hohen Materialverbrauch.

Mit unserer Nebenbedingung und durch Einsetzen des x-Wertes erhält man y = 15,811. Der kleinste Umfang U = x + 2y ist U = 63,244

Beispiel 2

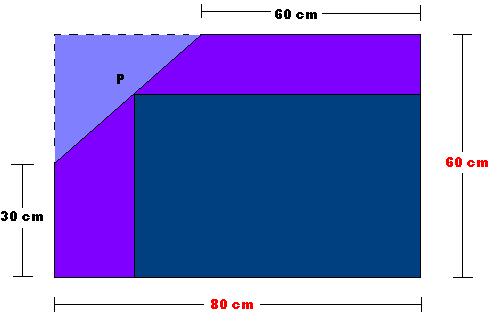
Bei einer rechteckigen Glasplatte ist eine Ecke abgebrochen (Fig. 1). Aus dem Rest soll eine rechteckige Scheibe mit möglichst großem Inhalt herausgeschnitten werden.
a) Wie ist Punkt P zu wählen?
b) Aus dem Rest soll wiederum eine rechteckige Scheibe herausgeschnitten werden. Wie groß kann diese höchstens werden?

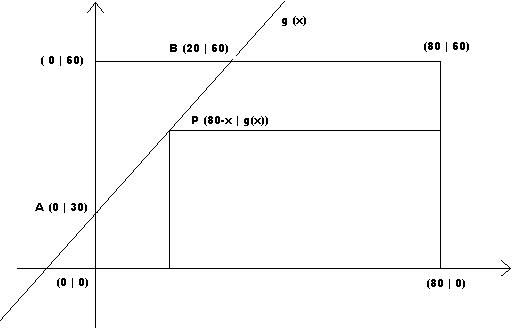
Problem skizzieren (Fig. 2) und ein KOS einführen.
Die Punkte A und B in g(x)= mx + n einsetzen um die Geradengleichung zu erhalten.

Für A in g(x) erhält man 30 = n und für B in g(x)erält man $\frac {3} {2}$ = m
Somit erhält man die Gerade g(x) = $\frac {3} {2}$ + 30

Beispiel 3

Aus einem kreisförmigen Rundstab mit dem Durchmesser d=12cm soll ein rechteckiger Stab mit einem möglichst großem rechteckigem Querschnitt gefertigt werden. Bestimmen Sie die Seitenlänge a und b des Rechtecks.

Lösung:

Leitfaden	Lösung am Beispiel
Angaben rausschreiben	geg.: Querschnitt von einem kreisförmigen Rundstab (Kreis) d=12cm ges.: Rechteck mit größtem Flächeninhalt
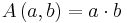
Zielfunktion aufstellen	$A\left( a,b \right)= a\cdot b$
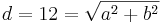
Nebenbedingungen	$d=12= \sqrt{a^2+b^2}$
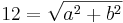
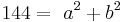
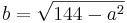
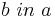
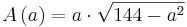
Nebenbedingungen ausnutzen	$12= \sqrt{a^2+b^2}$ $144=\ a ^2+b^2$ $b=\sqrt{144-a^2}$ $b\ in\ a$ $A\left( a \right)=a\cdot\sqrt{144-a^2}$
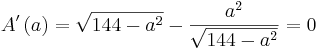
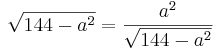
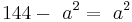
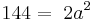
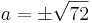
1.Ableitung aufstellen und = 0 setzen	$A\!\,'\left( a \right)=\sqrt{144-a^2}-\frac{a^2}{\sqrt{144-a^2}}= 0$ $\sqrt{144-a^2}= \frac{a^2}{\sqrt{144-a^2}}$ $144-\ a ^2=\ a ^2$ $144=\ 2a ^2$ $\ a=\pm \sqrt{72}$
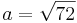
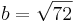Für die länge und Breite des Rechtecks ergibt sich somit: ---> $\ a= \sqrt{72}$ $\ b= \sqrt{72}$ } Beispiel 4 Wirtschaftsbezogene Aufgabe Seite 56 Aufgabe 6 Vor fünf Jahren hat eine Firma eine Werkzeugmaschine zum Preis von 60000€ gekauft. Statistische Daten sprechen für Gesamtreperaturkosten R mit der Geleichung: R(t)=(480+300t)t mit t in Jahren, R(t) in € a) Bestätigen Sie, dass für die Kosten K gilt: K(t)=R(t)+60000 b) Bestimmen Sie die Funktion, die die durschnittliche jährlichen Kosten angibt. Wann sollte die Firma die Werkzeugmaschine ausmustern? 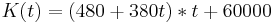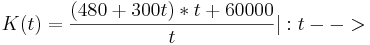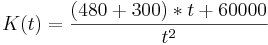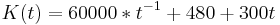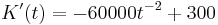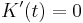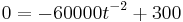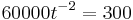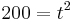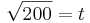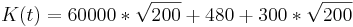Lösung zu a): $K(t)=(480+380t)t+60000$ Lösung zu b) $K(t)=\frac{(480+300t)t+60000}{t} \|:t -->$ Kosten = Gesamtreperaturkosten + Gewinn $K(t)=\frac{ (480+300)t+ 60000}{t^2}$ $K(t)= 60000t^{-1} + 480 + 300t$ $K'(t)= -60000t^{-2} +300$ ----> Nach t auflösen $K'(t)=0$ $0 = -60000t^{-2} + 300$ $60000t^{-2} = 300$ $200 = t^{2}$ $\sqrt{200} = t$ ---> Einsetzen in K (t) 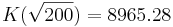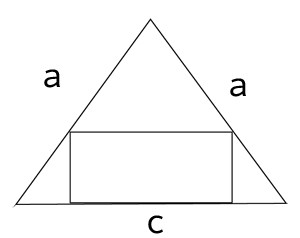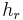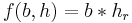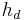$K(t)= 60000\sqrt{200} + 480 +300 * \sqrt{200}$ $K(\sqrt{200})= 8965.28$ Symmetrie beschreibt den Verlauf eines Graphen. Es gibt zwei verschiedene Symmetriearten. Einmal die Achsensymmetrie und zum anderen die Punktsymmetrie. Die Achsensymmetrie spiegelt den Graphen auf der y-Achse. Man geht folgendermaßen vor, um die y-Achsensymmetrie zu bestimmen: f(-x)= f(x) Hat man nun die Funktion f(x)=x⁴-4x²+10 gegeben, formt man die Funktion entsprechendermaßen nach f(-x)= f(x) um. (-x)⁴ -4(-x)²+10 = x⁴-4x²+10 Nun kann man erkennen, dass f(-x) gleich f(x) ist und somit auch feststellen, dass es sich um eine Funktion handelt, die achsensymmetrisch ist. Sind die Exponenten gerade kann man sagen, dass der Graph achsensymmetrisch sein muss. Die Punktsymmetrie erkennt man dadurch, dass sie durch den Koordinaten-Ursprung verläuft. Man geht folgendermaßen vor, um diese Symmetrie zu bestimmen. f(-x)=-f(x) Hat man die Funktion x⁵+x³+10, trägt man diese wieder in f(-x)=-f(x) ein. Sind beide Funktionsterme gleich, dann ist der Graph punktsymmetrisch. -(x)⁵-(x)³+10 = - (x⁵+x³+10) Sind die Exponenten ungerade kann man sagen, dass der Graph punktsymmetrisch ist. Beispiel 5 Aufgabe: Aus einer Holzplatte, die die Form eines gleichschenkligen Dreiecks mit den Seiten a=50 cm, c=60cm hat, soll ein möglichst großes rechteckiges Brett herausgeschnitten werden. Wie groß kann das Rechteck höchstens sein, wenn die Basis b genannt wird und die Höhe $h_r$ ? 1. Zielfunktion aufstellen: $f(b,h)=bh_r$ 2. Prüfen, ob Zielfunktion von Nebenbedingungen abhängt.* Man kann in diesem Fall die Strahlensätze zur Findung einer Nebenbedingung ausnutzen, die uns eine Variable in abhaengigkeit der Anderen angibt. 3. Nebenbedingung suchen Die Höhe $h_d$ des Dreiecks steht im Zusammenhang mit der Haelfte der Basis c, wie die Hoehe des Rechtecks $h_r$ zu dem Abschnitt x (zwischen der Basis des Rechtecks und dem Winkel) auf der Seite c $c$ : $\frac {h_d}{0,5c}= \frac {h_r}{x}$ Eine Termumformung liefert: $h_r=\frac {bh_d}{c}$ Wenn man diese ausnutzt ergibt sich die Funktion $f(b)=\frac {b^2h_d}{c}$ $h_d$ ist in diesem Fall eine aus dem Satz des Pythagoras bekannte Größe: 40 Die vollkommen ausformulierte Funktionsformel lautet nun: $f(b)=\frac{2b^2}{3}$ 4. Ableiten. $f'(b)=\frac{4b}{3}$ 5. Extrempunkte bestimmen . notwendige Bedingung fuer Extrema: f'(b)=0 6. Rand des Definitionsbereiches auf globale Extremstellen prüfen.