Funktionenscharen
Aus KAS-Wiki
Version vom 12. Dezember 2013, 10:23 Uhr von Haris Trgo (Diskussion | Beiträge)
|
|
|
|---|---|---|
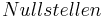
|
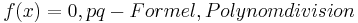
|
Ist die Nullstelle von t abhängig? Ja » Einschränkungen bezüglich t beachten: » Habe ich durch t dividiert ? » Habe ich die Wurzel aus t gezogen ? |
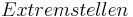
|
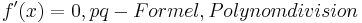
|
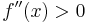 »Minimum; »Minimum; 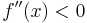 » Maximum, » Maximum, 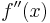 ≠ 0, sonst Sattelpunkt. Ist die Extremstelle von t abhängig ? Ja » Abgleich von t mit der Aufgabenstellung (Einschränkungen für t) » ist ≠ 0, sonst Sattelpunkt. Ist die Extremstelle von t abhängig ? Ja » Abgleich von t mit der Aufgabenstellung (Einschränkungen für t) » ist 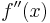 abhängig von t ? »» Dann Falluntersuchung ob ein Minimum oder Maximum vorliegt. abhängig von t ? »» Dann Falluntersuchung ob ein Minimum oder Maximum vorliegt.
|
|
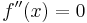 , pq-Formel; Polynomdivision , pq-Formel; Polynomdivision
|
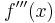 ≠ 0 sonst Ø Wendepunkt. Ist die Wendestelle von t abhängig ? »Ja wenn ... ≠ 0 sonst Ø Wendepunkt. Ist die Wendestelle von t abhängig ? »Ja wenn ...
|
|
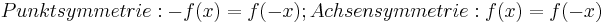
|
0) gehen. |
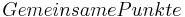
|
t1 und t2 mit t1 ≠ t2 einsetzen und dann gleichsetzen | t1 ≠ t2 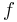
|
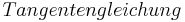
|
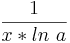
|
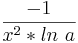
|
| Ortskurve der Extremstellen/Wendestellen | 1. Bestimmung der Extremstelle x, 2.Extremstelle in ft(x) einsetzen » nach y auflösen, Diex-Koordinate nach t auflösen und t in y-Koordinate einsetzen | Geht nur, wenn Extremstelle von x abhängig ist ! |

