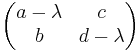Eigenwerte und Eigenvektoren (Fixelemente).
Aus KAS-Wiki
Version vom 14. Dezember 2009, 11:27 Uhr von Elizaveta (Diskussion | Beiträge)
Inhaltsverzeichnis[Verbergen] |
Definition
Eigenwerte
Eigenvektoren
Bestimmung von Eigenwerten
Gegeben ist die Abbildungsmatrix A=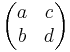 .
.
Aufstellen der charakteristischen Gleichung:
det(A-A)=0<=>(a-
)(d-
)-bc=0
Die Lösungen 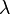 1/
1/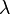 2 dieser Gleichung sind die Eigenwerte. Die charakteristische Gleichung hat eine, zwei oder keine Lösung.
2 dieser Gleichung sind die Eigenwerte. Die charakteristische Gleichung hat eine, zwei oder keine Lösung.
Bestimmung von Eigenvektoren
Die Eigenvektoren erhält man, indem man das LGS=
löst.
Für den Eigenwert 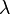 =1 erhält man eine Fixpunktgerade, für
=1 erhält man eine Fixpunktgerade, für 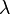
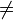 1 eine Fixgerade.
1 eine Fixgerade.
Beispielaufgaben
Bestimmung der Eigenwerte:
Gegeben ist die Matrix A=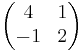
Aufstellen der charakteristischen Gleichung:
(4-)(2-
)+1=0 <=>
2-6
+8+1=0 <=>
2-6
+9=0 <=>
1/2=3
<=>
1/2=3
=>d.h. nur ein Eigenwert
Bestimmung des Eigenvektors: