Extremwertaufgaben.

Definition:

Extremwertprobleme sind Aufgaben bei denen mithilfe von einer Hauptbedingung und einer Nebenbedingung eine Funktion aufgestellt werden kann die anschließend auf Extremstellen untersucht wird. (Kurvendiskussion)

Lösungsansatz:

1. Zielfunktion aufstellen.
2. Prüfen ob Zielfunktion von Nebenbedingungen abhängt.
3. Nebenbedingung suchen (Um Variablen in Beziehung zu bringen).
4. Ableiten. (Ableitungsregeln.)
5. Extrempunkte bestimmen (Extrempunkte).
6. Rand des Definitionsbereiches auf globale Extremstellen prüfen. (Grenzverhalten)

Beispiele

Beispiel 1

Ein Schäfer benötigt für seine Schafherde ein rechteckigen Pferch mit einem Flächeninhalt von 500m². Wie soll er die Maße des Rechtecks wählen, damit für eine Umzäunung möglichst wenig Material benötigt wird, wenn eine Rechteckseite von einem Bach gebildet wird?

Lösung:

1. Die gesuchte Zielfunktion soll die Seitenlängen des Zauns angeben bei denen ein möglichst geringer Materialverbrauch, also ein möglichst kleiner Umfang, entsteht. Des Weiteren soll eine Fläche von 500 m² entstehen. Der Umfang ist abhängig vom Flächeninhalt, die Zielfunktion ist also auch abhängig von einer Nebenbedingung.
2. Die Nebenbedingung, dass eine Fäche von 500 m² enstehen soll ist durch die einfach multiplikation der beiden Seiten x und y ausrückbar: 500 = x * y
3. Die Formel mit der man den Umfang eines Rechteckes ausdrückt ist U = 2x + 2y. In der gestellten Aufgabe wird jedoch eine Seite von einem Bach begrenzt, es ist also nicht nötig an dieser Seite einen Zaun zu bauen. Deshalb ergibt sich für die Länge des Zaunes: U = x + 2y Löst man die bereits aufgestellte Nebenbedingung 500 = x * y nach y auf erhält man 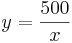$y = \frac {500} {x}$. Nach einsetzen in U = x + 2y ergibt sich unsere Zielfunktion: $U(x) = x + \frac {1000} {x}$.
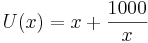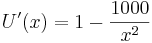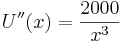4. Die Ableitungen der Funktion sind: $U'(x)=1-\frac {1000} {x^2}$ und $U''(x)= \frac {2000} {x^3}$. Für U' (x) = 0 erhält man x = 31,622 das sich aufgrund der Bedingung U (31,622) > 0 als Tiefpunkt heraustellt.
5. Mit unserer Nebenbedingung und durch einsetzten des x-Wertes erhält man y = 15,811. Der kleinste Umfang U = x + 2y ist U = 63,244