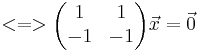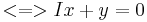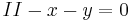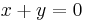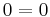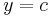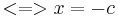Eigenwerte und Eigenvektoren (Fixelemente).: Unterschied zwischen den Versionen

Aus KAS-Wiki
Wechseln zu: Navigation, Suche
(→‎Beispielaufgaben)
K (→‎Beispielaufgaben)
Zeile 46: Zeile 46:
  
 
                                           <math>(A-\lambda E)\vec x=\vec 0\!\,</math>
 
                                           <math>(A-\lambda E)\vec x=\vec 0\!\,</math>
−
                                     <math><=>[\begin{pmatrix} 4 & 1 \\ -1 & 2 \end{pmatrix} -\begin{pmatrix} 3 & 0 \\ 0 & 3\end{pmatrix}]\vec x=\vec 0\!\, </math>
+
                                     <math><=>\left[\begin{pmatrix} 4 & 1 \\ -1 & 2 \end{pmatrix} -\begin{pmatrix} 3 & 0 \\ 0 & 3\end{pmatrix}\right]\vec x=\vec 0\!\, </math>
 +
                                    <math><=>\begin{pmatrix} 1 & 1 \\ -1 & -1 \end{pmatrix}\vec x=\vec 0\!\,</math>
 +
 
 +
                                    <math><=>I x+y=0\!\,</math>
 +
                                          <math>  II -x-y=0\!\,</math>
 +
 
 +
                                          <math>x+y=0\!\,</math>
 +
                                          <math>0=0\!\,</math>
 +
 
 +
                                          <math>y=c\!\,</math>
 +
                                    <math><=> x=-c\!\,</math>

Version vom 14. Dezember 2009, 12:08 Uhr

Inhaltsverzeichnis

Definition

Eigenwerte

Eigenvektoren

Bestimmung von Eigenwerten

Gegeben ist die Abbildungsmatrix A=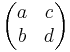\begin{pmatrix} a & c\\ b & d \end{pmatrix}.

Aufstellen der charakteristischen Gleichung: 

                     det(A-\lambdaA)=0<=>(a-\lambda)(d-\lambda)-bc=0

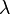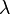Die Lösungen \lambda1/\lambda2 dieser Gleichung sind die Eigenwerte. Die charakteristische Gleichung hat eine, zwei oder keine Lösung.

Bestimmung von Eigenvektoren 

Die Eigenvektoren erhält man, indem man das LGS \begin{pmatrix}
a-\lambda & c \\
b & d-\lambda
\end{pmatrix} \vec x=\vec0 löst.

Für den Eigenwert 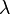\lambda=1 erhält man eine Fixpunktgerade, für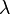 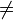\lambda\ne1 eine Fixgerade.

Beispielaufgaben

Bestimmung der Eigenwerte:

Gegeben ist die Matrix 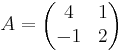A=\begin{pmatrix} 4 & 1 \\ -1 & 2 \end{pmatrix}\!\,

Aufstellen der charakteristischen Gleichung: 

                                           (4-\lambda)(2-\lambda)+1=0\!\,
                                     <=>\lambda^2-6\lambda+8+1=0\!\,
                                     <=>\lambda^2-6\lambda+9=0\!\,
                                     <=>\lambda_{1,2}=3\pm\sqrt{9-9}\!\,
                                     <=>\lambda_{1,2}=3\!\,

=>d.h. nur ein Eigenwert

Bestimmung des Eigenvektors: 

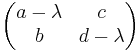
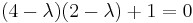
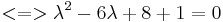
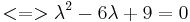
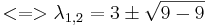
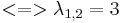
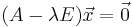
                                          (A-\lambda E)\vec x=\vec 0\!\,
                                    <=>\left[\begin{pmatrix} 4 & 1 \\ -1 & 2 \end{pmatrix} -\begin{pmatrix} 3 & 0 \\ 0 & 3\end{pmatrix}\right]\vec x=\vec 0\!\, 
                                    <=>\begin{pmatrix} 1 & 1 \\ -1 & -1 \end{pmatrix}\vec x=\vec 0\!\,

                                    <=>I x+y=0\!\,
                                             II -x-y=0\!\,

                                          x+y=0\!\,
                                          0=0\!\,

                                          y=c\!\,
                                    <=> x=-c\!\,
Von „http://kas.zum.de/index.php?title=Eigenwerte_und_Eigenvektoren_(Fixelemente).&oldid=928“