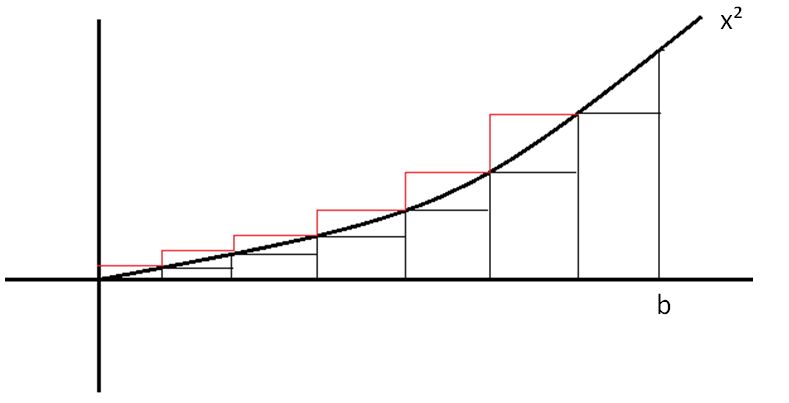
Produktsummen

h= Breite des Rechtecks
$h=\frac{b}{n}$
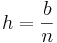
b= Grenze
n= Anzahl der Rechtecke

Im Folgendem stelle ich den Bezug zwischen der Produktsumme und der Flächeninhaltsfunktion her. Dabei beziehe ich mich auf die oben abgebildete Grafik.
Wählt man die Höhe so, dass 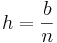$h=\frac{b}{n}$ kann man die Untersumme folgendermaßen bestimmen:
sn= 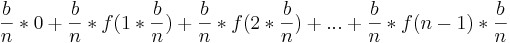$\frac {b}{n}*0+\frac {b}{n}*f(1*\frac {b} {n})+ \frac {b}{n}*f(2*\frac {b}{n})+ ... + \frac {b}{n}*f(n-1)*\frac {b}{n}$

Die Formel setzt sich ganz einfach zusammen. Um die Fläche eines gewählten Balkens unter dem Graphen von 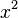$x^2$ zu berechnen, benutzt man die Formal zur Rechtecksberechnung.
In diesem Fall multipliziert man 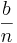$\frac{b}{n}$ mit dem Funktionswert f von 1*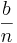$\frac{b}{n}$. Um auf die Untersumme zu gelangen addiert man jeweils alle Streifen miteinander bis zur Grenze b.
Man fragt sich jetzt sicherlich warum 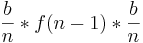$\frac {b}{n}*f(n-1)*\frac {b}{n}$ als letztes steht.
Auch das ist klar zu verstehen, wenn man die obenstehende Grafik betrachtet:
Man erkennt, dass die Grenze, bis zu der wir die Fläche unter dem Graphen bestimmen wollen bei b liegt. Diese Grenze liegt bei der Untersumme bei 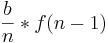$\frac{b}{n}*f(n-1)$, d.h. mit 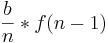$\frac{b}{n}*f(n-1)$ berechnet man den letzten Streifen unter dem Graphen.

Setzt man jetzt 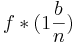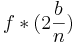$f*(1\frac{b}{n})$, $f*(2\frac{b}{n})$ usw. in die Funktion 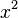$x^2$ ein, so kommt man auf folgenden nächsten Schritt:
sn= $\frac {b}{n}*[1^2\frac {b^2}{n^2}+ 2^2\frac {b^2}{n^2}+ ... + (n-1)^2\frac {b^2}{n^2}]$
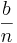Ich habe $\frac {b}{n}$ dabei ausgeklammert.
Im nächsten Schritt kann man weiterhin 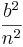$\frac {b^2}{n^2}$ vor die Klammer schreiben und man kommt zu folgender Schlussfolgerung:

sn= 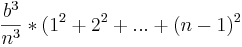$\frac {b^3}{n^3}*(1^2+2^2+ ... + (n-1)^2$
Jetzt kommt die Formel für die Summe der ersten n-Quadratzahlen zum Gebrauch:
$1^2+2^2+...+n^2= \frac {1}{6}*n(n+1)*(2n+1)$

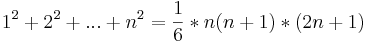
Daraus folgt dann die Weiterführung dieser Formel: sn= 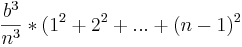$\frac {b^3}{n^3}*(1^2+2^2+ ... + (n-1)^2$
Für die Untersumme gilt (n-1), also setzt man für n=(n-1) ein.
Das sieht folgendermaßen aus:
sn=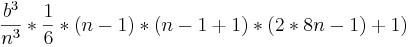$\frac {b^3}{n^3}*\frac{1}{6}*(n-1)*(n-1+1)*(2*8n-1)+1)$
Zur Veranschaulichung werde ich diesen Term einmal Schritt für Schritt vereinfachen:
=$\frac{1}{6}*\frac {b^3}{n^3}*(n-1)*n*(2n-1)$ =$\frac{1}{6}*b^3(\frac{n-1}{n})*(\frac{n}{n})*(\frac{2n-1}{n})$ =$\frac{1}{6}*b^3*(1-\frac{1}{n})*(2-\frac{1}{n})$
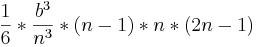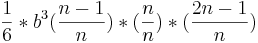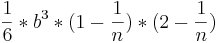
Man sieht, dass die Balken unter dem Graphen immer Größer werden und der Flächeninhalt nicht genau bestimmt werden kann, also bestimmt man das Verhalten in das Unendliche:
$lim (n)--> Unendlich$ $\frac{1}{6}*b^3*1*2=\frac{1}{3}*b^3$
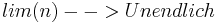
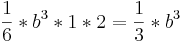
Nun fällt auf, dass 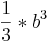$\frac{1}{3}*b^3$ die Aufleitung von 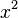$x^2$ ist und man hat fast nachgewiesen, dass die Produktsumme offensichtlich einen Bezug zur Stammfunktion darstellt.
Man muss nämlich noch die Obersumme in Betracht ziehen und das geschieht im Folgendem:
Es ist wesentlich einfacher diese Obersumme zu bestimmen, da die Höhe von der Obersumme mit der Grenze b übereinstimmt. Das heißt, dass man die Formel 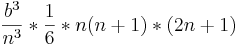$\frac{b^3}{n^3}*\frac {1}{6}*n(n+1)*(2n+1)$ nur vereinfach muss:
=$\frac {1}{6}*b^3*\frac {n}{n}*(\frac {n+1}{n})*(\frac {2n+1}{n}) =\frac {1}{6}*b^3*(1+\frac {1}{n})*(2+\frac {1}{n})$
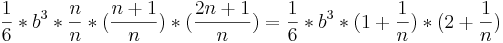
Nun wieder das Verhalten ins Unendliche überprüfen:
$lim(n) --> Unendlich \frac {1}{6}*b^3*1*2=\frac {1}{3}*b^3$

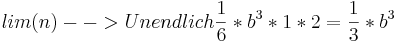
Ober- und Untergrenze sind somit gleich 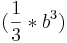$(\frac {1}{3}*b^3)$ und die Fläche unter dem Graphen von 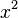$x^2$ ist genau $(\frac {1}{3}*b^3)$.
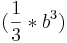Somit ist der Bezug von Produktsume zur Flächeninhaltsfunktion vollständig hergestellt und die Flächenberechnung kann durch die Aufleitung geschehen.