Proportionalitäten erkennen
Funktionale Zusammenhänge + physikalische Größen aus einem Experiment ableiten
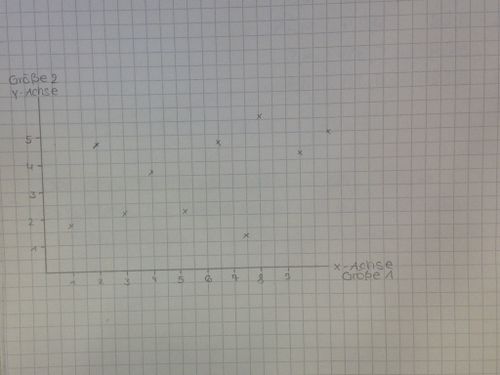
Wenn zwei Größen funktional zusammenhängend sind, dann verändern sich die Größen immer verhältnismäßig gleich zueinander. Beispiel A: Addiert man zu Größe 1 den Wert 2, addiert sich zur Größe 2 auch der Wert 2. Dies trifft bei linearen Funktionen zu.
Beispiel B: Verdoppelt man Größe 1, verdoppelt sich auch Größe 2. Dies trifft nur bei proportionalen Funktionen zu.
Nicht erkennbar als linearer Graph:
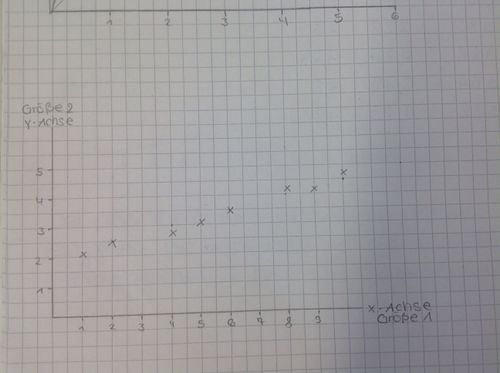
Beispiel für eine lineare Funktion:
| Größe 1 | Größe 2 |
|---|---|
| 2 | 2,5 |
| 4 | 3 |
| 6 | 3,5 |
| 8 | 4 |
| 10 | 4,5 |
Eingezeichnete Punkte einer linearen Funktion:
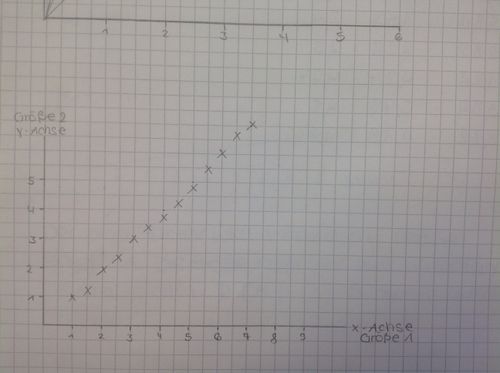
Beispiel für eine proportionale Funktion:
| Größe 1 | Größe 2 |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
Eingezeichnete Punkte einer proportionalen Funktion:
Zunächst wurden von uns zwei physikalische Größen gemessen, wobei wir bewusst eine Größe verändert und die andere gemessen haben, die Messwerte haben wir dann in eine Wertetabelle eingetragen. Die Größen haben wir danach in einem Koordiantensystem jeweils auf der x- und y-Achse eingezeichnet und nun werden Punkte im Koordinatensystem markiert, die den gemessenen Werten entsprechen. Dann wird ein Graph in Form einer Gerade gezogen. Falls man von einer proportionalen Funktion ausgeht, zieht man eine Gerade vom Nullpunkt aus, welche möglichst viele Messpunkte überschneidet, wobei sich die Steigung errechnen lässt, wenn man Wert x mit dem entsprechenden Wert y dividiert. Geht man jedoch von einer quadratischen Funktion aus, quadriert man die eine Größe und teilt sie durch die andere Größe, aus welcher sich die Steigung ergibt.
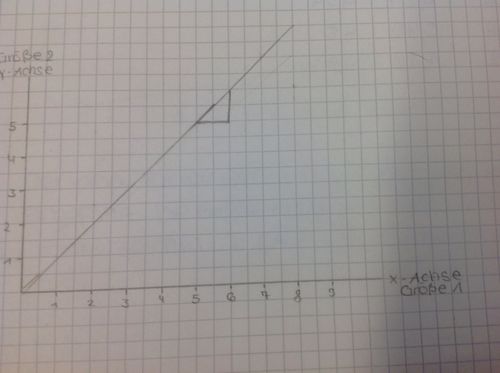
Daraufhin wird das Steigungsdreieck errechnet/abgelesen. Das Steigungsdreieck errechnet man, indem man schaut, um wie viel sich das y verändert, wenn sich x um eins erhöht. Die Steigung beschreibt, um wie viel der y-Wert pro x sich verändert.
Hierbei beträgt die Steigung 1, denn wenn x um 1 erhöht wird erhöht sich auch y um genau 1.
Daraus kann man den Funktionsterm y=mx bilden, wobei m für die Steigung des Graphen steht. Die neu entstandene physikalische Größe kann errechnet werden, indem man x durch y teilt.