Quadratische Ergänzung

Die quadratische Ergänzung ist ein Verfahren zum Umformen von Termen. Sie dient zum Beispiel dazu, quadratische Gleichungen zu lösen oder zur Bestimmung der Scheitelpunktsform von quadratischen Funktionen. Lösen einer quadratischen Gleichung: (x+5)(x-12)=5(4-x)

x²-12x+5x-60=20-5x

x²-60-7x=20-5x

x²-80-2x=0

x²-2x+1-1-80=0

(x-1)²-81=0

(x-1)²=81

x-1=9 v x-1=-9

X=10 v x=-8

Lösungsmenge: {10;-8}

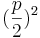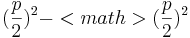Formel: ²+px+q=0 ²+px+$(\frac{p}{2})^2$-(\frac{p}{2})^2</math>+q=0 (x+$(\frac{p}{2})^2-<math>(\frac{p}{2})^2$+q=0

Beispiel: x^2+4x-12=0/QE x^2+4x+4-4-12=0 (x+2)^2-16=0/+16 (x+2)^2 =16/Wurzel ziehen x+2=4 v. x+2=-4/-2 x=2 v. x=-6 Lösungsmenge:{-6;2}

Probe: -6^2+4*(-6)-12=0 36-24-12=0 0=0

2^2+4*2-12=0 4+8-12=0 0=0

Die quadratische Ergänzung

Die quadratische Ergänzung ist ein Verfahren zum Umformen von Termen. Sie dient zum Beispiel dazu, quadratische Gleichungen zu lösen oder zur Bestimmung der Scheitelpunktsform von quadratischen Funktionen. Lösen einer quadratischen Gleichung: x²+20x+125=0

x²+20x+125=0          |+100-100 Als ersten Schritt muss man immer eine Zahl hinzufügen bzw. Zahlen ( + x und - x ),

                      damit man eine binomische Formel zusammenfassen kann, in diesem Fall ist es + 100 - 100, 
                      da die 100 die ( 1.) binomische Formel ergänzt. ( x²+20x+100 → (x+10)²
                      
                      

x²+20x+100-100+125=0

(x+10)²-100-125=0

(x+10)²-225=0         |+225

(x+10)²=225           |√

x+10=15 oder x=-15    |-10

x=15-10 oder x=-15-10

x=5     oder x=-5