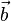Skalarprodukt, Vektorprodukt.
Inhaltsverzeichnis[Verbergen] |
Skalarprodukt
Mit dem Skalarprodukt berechnet man den Winkel zwischen zwei Vektoren.
Die allgemeine Formel lautet : 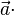 *
*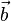 =
=  *
*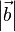 * cos
* cos 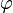
Um den Winkel zwischen zwei Vektoren auszurechnen, formt man die Formel um in
cos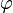 =
=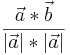
Beispiel 1
Berechne den Winkel zwischen den Vektoren 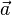 =
=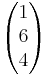 und
und  =
= 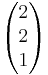
Also cos  =
=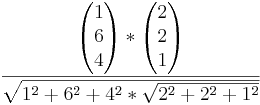 =
= 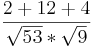 =
=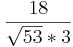 =
=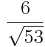 daraus folgt
daraus folgt 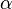
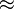 34,5°
34,5°
Aber Vorsicht: Man muss die Richtung des Vektors beachten sonst rechnet man nicht den gewünschten Winkel aus. Mit a*b kann man sowohl den Innenwinkel (siehe Bild 1) als auch den aussen Winkel(siehe Bild 2)ausrechnen,also immer die Richtung des Vektors beachten.
Orthogonalität
Wenn 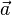 und
und 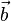 mit a
mit a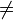 0 und b
0 und b 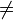 0 sind und es gilt:
0 sind und es gilt: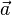 *
*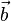 = 0
dann bedeutet es, dass
= 0
dann bedeutet es, dass 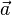 und
und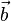 orthogonal zueinander sind.
orthogonal zueinander sind.
Beispiel 2
Prüfe,ob die Vektoren a=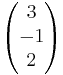 und b=
und b=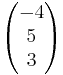 orthogonal (rechtwinklig) sind
orthogonal (rechtwinklig) sind
Bedingung ist 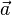 *
*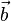 muss gleich 0 sein
muss gleich 0 sein
Also :
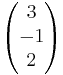 *
* = 3* (-4) + (-1) * 5 + 2 * 3= -11
= 3* (-4) + (-1) * 5 + 2 * 3= -11
und -11 ist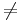 0, deswegen sind
0, deswegen sind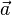 und
und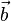 nicht orthogonal
nicht orthogonal
Vektorprodukt oder auch Kreuzprodukt
Mit dem Vektorprodukt rechnet man den Vektor aus, der zu 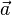 und
und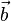 orthogonal ist
orthogonal ist
Formel für den 3 dimensionalen Raum
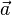
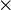
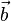 =
= 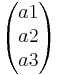
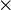
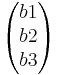 =
=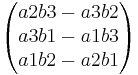
Beispiel 3
Bestimmen Sie alle Vektoren  , die zu
, die zu 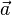 und
und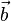 orthogonal sind
orthogonal sind
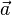 =
=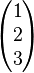 und
und 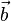
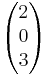
 =
=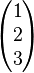
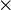
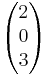 =
=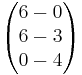 =
=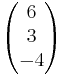
Also ist der Vektor 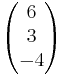 sowohl senkrecht zu
sowohl senkrecht zu 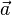 als auch zu
als auch zu