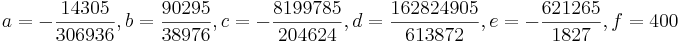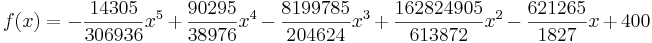Steckbriefaufgaben.

Allgemeines

Bei Steckbriefaufgaben geht es darum, Funktionen mithilfe von Nebenbedingungen, wie z.B. Punkten, Extremstellen, etc., zu bestimmen. Dabei werden diese Nebenbedingungen in Textform angegeben. Zur Lösung von Steckbriefaufgaben müssen die Nebenbedingungen aus dem Text herausgefiltert und in mathematischer Form dargestellt werden. Danach wird mit den mathematischen Nebenbedingungen ein lineares Gleichungssystem aufgestellt mit dessen Lösung man die Funktion bestimmen kann.

Beispielaufgabe

Verkehrszählung am Hauptbahnhof

Im Zusammenhang mit der Diskussion um die Feinstaubbelastung am Graf-von-Galen-Ring in Hagen wurden auch umfangreiche Verkehrszählungen durchgeführt. Ich habe die meisten Zahlen, die bei der Diskussion im Umweltausschuss genannt wurden, nicht behalten, aber an folgende Datenlage erinnere ich mich noch: An einen Wochentag hatten wir um 0 Uhr morgens eine Verkehrsdichte von 400 Kfz/h, der höchste Wert lag um 8 Uhr bei 2100 Kfz/h. Danach sank die Verkehrsdichte bis 14 Uhr auf 1600 Kfz/h und stieg dann wieder auf ein Zwischenhoch um 17 Uhr.

b) Bestimmen Sie eine ganzrationale Funktion, die die Verkehrsdichte (in Kfz/h) in Abhängigkeit von der Tageszeit (in h) gemäß den oben angegebenen Daten beschreibt.

Diese Aufgabe ist entnommen von der Aufgabensammlung(Reader) auf dieser Seite:[1], 8.12.2009

Rechnung

Bei dieser Aufgabe wird eine Funktion gesucht, welche die Verkehrsdichte (in Kfz/h) am Graf-von-Galen-Ring in Abhängigkeit von der Tageszeit angibt. Dies bedeutet der 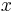$x\!\,$-Wert der Funktion gibt die Uhrzeit an und der Wert von 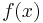$f\!\,(x)$ die Verkehrsdichte.

Nebenbedingungen aufstellen

Aus dem Text lassen sich folgende Nebenbedingungen herausfiltern:

• I.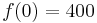$f\!\,( 0 )=400$, da um 0 Uhr eine Vehrkersdichte von 400 Kfz/h herrschte.
• II.$f\!\,(8)=2100$, da die Verkehrsdichte um 8 Uhr bei 2100 Kfz/h lag.
• III.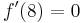$f\!\,'(8)=0$, da der Wert um 8 Uhr zudem der höchste am Tag ist hat 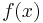$f\!\,(x)$ hier ein Maximum.
• IV.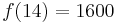$f\!\,(14)=1600$, weil wie im Text erwähnt um 14 Uhr die Verkehrsdichte bei 1600 Kfz/h lag.
• V.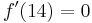$f\!\,'(14)=0$, weil gesagt wird, dass die Verkehrsdichte bis 14 Uhr sankt und danach wieder stieg, muss bei 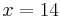$x\!\,=14$ ein Minimum liegen.
• VI.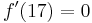$f\!\,'(17)=0$, weil im Text von einem Zwischenhoch um 17 Uhr die Rede ist, liegt bei 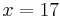$x\!\,=17$ ein Maximum.

Da man mit 6 Nebenbedingungen eine ganzrationale Funktion von höchstens fünftem Grad bestimmen kann lautet die allgemeine Funktion:

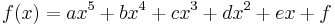• $f\!\,(x)=ax^5+bx^4+cx^3+dx^2+ex+f$ mit
• $f\!\,'(x)=5ax^4+4bx^3+3cx^2+2dx+e$

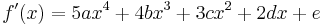
Gleichungssystem aufstellen

Aus diesen mathematischen Nebenbedingungen lässt sich nun folgendes lineares Gleichungssystem aufstellen:

• I.$0a+0b+0c+0d+0e+f=400<=>f=400\!\,$
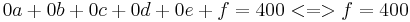
• II.$32768a+4096b+512c+64d+8e+400=2100\!\,$
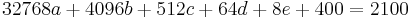
• III.$20480a+2048b+192c+16d+e=0\!\,$
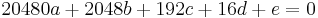
• IV.$537824a+38416b+2744c+196d+14e+400=1600\!\,$
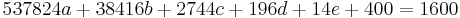
• V.$192080a+10976b+588c+28d+e=0\!\,$
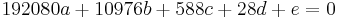
• VI.$417605a+19652b+867c+34d+e=0\!\,$

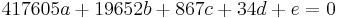
Lösen des Gleichungssystems

Mit Hilfe eines Computer Algebra Systems folgt aus diesem Gleichungssystem die Lösung:

• SOLVE([0·a + 0·b + 0·c + 0·d + 0·e + f = 400, 32768·a + 4096·b + 512·c + 64·d + 8·e + f = 2100, 20480·a + 2048·b + 192·c + 16·d + e = 0, 537824·a + 38416·b + 2744·c + 196·d + 14·e + f = 1600, 192080·a + 10976·b + 588·c + 28·d + e = 0, 417605·a + 19652·b + 867·c + 34·d + e = 0], [a, b, c, d, e, f])

• $a = -\frac {14305} {306936}, b =\frac {90295} {38976}, c = -\frac {8199785} {204624}, d =\frac {162824905} {613872}, e = -\frac {621265} {1827}, f = 400\!\,$

Somit lautet die ganzrationale Funktion, welche die Verkehrsdichte (in Kfz/h) in Abhängigkeit von der Tageszeit angibt:

• $f(x)=-\frac {14305} {306936}x^5+\frac {90295} {38976}x^4-\frac {8199785} {204624}x^3+\frac {162824905} {613872}x^2-\frac {621265} {1827}x+400\!\,$

Bei dieser Aufgabe ist es komfortabler ein Computer Albgebra System für die Lösung des Gleichungssystems zu benutzen, da das Gleichungssystem hohe Koeffizienten und eine hohe Anzahl an Variablen besitzt. Es würde sehr lange dauern es eigenständig zu lösen. Einfachere Gleichungssysteme können aber auch mit bestimmten Methoden gut selbstständig gelöst werden, siehe dafür Lösung linearer Gleichungssysteme..

Formulierungsbeispiele

Im folgenden werden einige typische Formulierungsbeispiele für Nebenbedingungen in Textform und deren mathematische Übersetzung genannt.

• Der Graph von 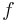$f\!\,$ berührt bei 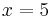$x=5\!\,$ die x-Achse.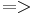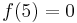$=>$ $f(5)=0\!\,$ und $f\!\,'(5)=0\!\,$
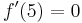
• Der Graph von 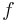$f\!\,$ hat bei 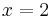$x=2\!\,$ eine Wendetangente mit der Steiogung 4.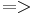 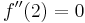$=>$ $f\!\,''(2)=0\!\,$ und $f\!\,'(2)=4\!\,$
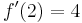
• Element C

Weblinks für weitere Aufgaben

• [2]
• [3], zur Überprüfung der errechneten Ergebnisse